Freudenthal begins by taking a ratio to be a function of an ordered pair of numbers (the ratio of 3 and 4 is 3:4). But this definition is too close to the notion of quotient, which he says is different from a ratio (logically or phenomenologically?). To interpret ration in terms of quotient is to “deprive it of what it makes valuable as ratio”. So he reinterprets ratio as an equivalence relation in the set of ordered pair of numbers indicated formally as a:b = c:d.

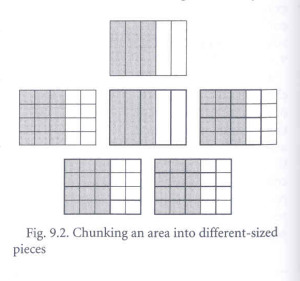
Lamon begins by describing  different ways of chunking quantities that often people use during their shopping time. Children chunk information into pieces that are either easy for them to think about or the once that they have experience with. The ability to re-conceptualize quantities in different chunks adds flexibility and usefulness to ones knowledge.

However, in the school syllabus only one kind of chunking is emphasized, called as “unitary method”, where often students are expected to find value/price of a unit to find the values of multiple units. Lamon thinks that one should take the benefit of the students’ natural ability of chunking in fraction instruction. She defines unitizing as follows:

Unitizing – The process of mentally constructing different sized chunks in terms of which to think about the given commodity is known as unitizing.

Let us see an example of unitizing in finding names for 3/5

3 (columns)/ 5 (columns)
= 12 (1×1 squares)/ 20 (1×1 squares)
= 1 ½ ( 1 × 2 rectangles) / 2 ½ (1 × 2 rectangles)
= 3 (2 × 2 squares) / 5 (2 × 2 squares)
= 2 (2 × 3 rectangles) / 3 1/3 (2 × 3 rectangles)
= 6 (1 × 2 rectangles) / 10 (1× 2 rectangles)

Three fifth is 3 out of 5 columns , it is 12 out of 20 small squares. In all the above representations the  area has remain unchanged, what has changed is the unit of measuring that area.

Unitizing has some advantages over part-whole:

• Unitizing involves similar processes as measurement
• Unitizing provides freedom to change the units, therefore making the learning of rules more flexible.
• Every student’s chunk/unit size vary, and that provides window in their thinking.
• Students become comfortable with complex fractions

Students experience with fractions and ratios begins before schooling. Mathematically successful students manage to connect this constructed knowledge with instructed knowledge(taught knowledge). Fraction is a mathematical idea which represents many kinds of relationship. A fraction ‘a/b’ is referred by the term ‘quotient’ if the meaning of ‘a/b’ is ambiguous and by ‘fraction’, ‘a/b’ indicates that ‘a’ things are equally divided among ‘b’ people. ‘a/b’ referred to ratio when it is a quotient with multiplicative relationship between two quantities and if it is reasoning with ratio ‘a/b’ referred to be ‘proportion or proportionality’.
The idea of fraction in children arise when the student started doing social activities. The concept of fair sharing gives the idea of equal partitioning. In sharing three things has to be taken care off.

1.each one should get a share

2.the shares must be of equal in size

3.shares taken together must exhaust a whole

Students will be able to do smaller number of partition easier because they can imagine it and it is difficult to do bigger number of partition.because it is very difficult to imagine. Chances should be given to given to connect their imagination with drawing or other representation and opportunities should be provided using ready made materials like fraction strip and fraction tile to make out more imagination at relevant times.
Children’s knowledge of fraction should move through making meaning for fraction by linking quotient to divided quantity and exploring mathematical properties of fraction as numbers. If students starts using fraction in quotient they need to learn the official names numerator and denominator. But it is very difficult to understand the meaning of two numerical component by its position. First students need to know the fraction size is dependent upon the size of the whole. In the case of fraction in terms of divided quantities students should know that the parts should be in equal size. They should also feel comfort to do the parts of discrete quantities as fraction.

If the students are ready to explore fractions as a system of numbers, the time should be invested to know the aspects of equivalent fractions and order of fraction. If they came to know these concepts clearly they can handle arithmetic of fraction and the range of practical application of these ideas in everyday life will be vast.
The comparison of fraction is done by four different methods

1.Divided quantities:- by making pictures

2.Numerical component:- by checking the missing area

3.Reference point:- by checking greater than or less than a particular point like ½,1/4.

4.Numerical conversion:- by taking LCM

While starting the concept of addition students generally make mistake like a/b+c/d=(a+c)/(b+d). This can be corrected by making drawings of addends and doing addition pictorially. In the real procedure of addition students may ask doubt like why do we have to change the denominator before addition. This can be clarified either by the concept of multiplicative identity or by connecting the change in the addend denominators to subdivision parts in addend quantities.

A quotient numeral of the form ‘a/b’ is used to name a fraction as well as ratio. Here the term ratio is used to describe a relational number that has two properties.

1.it relates two quantities in one situation.
2.It projects that the relationship into a second situation in which the relative amount of two quantities remains same.